Linear Algebra and the C Language/a0b3

/* ------------------------------------ */
/*  Save as :   c00a.c                  */
/* ------------------------------------ */
#include "v_a.h"
/* ------------------------------------ */
/* ------------------------------------ */
#define RA   R4
#define CA   C3 
#define Cb   C1 
/* ------------------------------------ */       
/* ------------------------------------ */
int main(void)
{
double ta[RA*(CA+Cb)]={
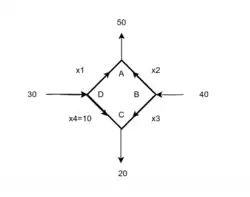
//  x1    x2    x3       
    +1,   +1,   +0,// A
    +0,   -1,   -1,// B
    +0,   +0,   +1,// C
    -1,   +0,   +0 // D  
};

double tb[RA*(CA+Cb)]={
     +50,   // A
     -40,   // B
 +20 -10,   // C
 -30 +10    // D  
};
                       
double **A      =   ca_A_mR(ta,i_mR(RA,CA));
double **b      =   ca_A_mR(tb,i_mR(RA,Cb));

double **Q      =              i_mR(RA,CA);
double **Q_T    =              i_mR(CA,RA);

double **R      =              i_mR(CA,CA);
double **invR   =              i_mR(CA,CA);

double **invR_Q_T = i_mR(CA,RA);
double **x        = i_mR(CA,C1); 

  clrscrn();
  printf(" Copy/Paste into the octave windows \n\n");
  p_Octave_mR(A,"a",P0);  
  printf(" [Q, R] = qr (a,0) \n\n");
  
  QR_mR(A,Q,R);    
  printf(" Q :");
  p_mR(Q, S10,P4, C10);  
  printf(" R :");
  p_mR(R, S10,P4, C10); 
  stop(); 
  
  clrscrn();
  transpose_mR(Q,Q_T);   
  printf(" Q_T :");
  pE_mR(Q_T,S9,P5, C3);
  invgj_mR(R,invR); 
  printf(" invR :");
  pE_mR(invR,S9,P5, C6);
  stop();

  clrscrn();
  printf(" Solving this system yields a unique\n"
         " least squares solution, namely   \n\n");
  mul_mR(invR,Q_T,invR_Q_T);
  mul_mR(invR_Q_T,b,x);
  printf(" x = invR * Q_T * b :");
  p_mR(x,S9,P5 ,C6);
  stop();
         
  f_mR(A);
  f_mR(b);
  f_mR(Q);
  f_mR(Q_T);
  f_mR(R);
  f_mR(invR);
  f_mR(x);
      
  return 0;
}
/* ------------------------------------ */
/* ------------------------------------ */

 Copy/Paste into the octave windows 

 a=[
+1,+1,+0;
+0,-1,-1;
+0,+0,+1;
-1,+0,+0]

 [Q, R] = qr (a,0) 

 Q :
   +0.7071    +0.4082    -0.2887 
   +0.0000    -0.8165    -0.2887 
   +0.0000    +0.0000    +0.8660 
   -0.7071    +0.4082    -0.2887 

 R :
   +1.4142    +0.7071    +0.0000 
   +0.0000    +1.2247    +0.8165 
   +0.0000    +0.0000    +1.1547 

 Press return to continue. 


 Q_T :
+7.07107e-01 +0.00000e+00 +0.00000e+00 
+4.08248e-01 -8.16497e-01 +0.00000e+00 
-2.88675e-01 -2.88675e-01 +8.66025e-01 

-7.07107e-01 
+4.08248e-01 
-2.88675e-01 

 invR :
+7.07107e-01 -4.08248e-01 +2.88675e-01 
-0.00000e+00 +8.16497e-01 -5.77350e-01 
-0.00000e+00 -0.00000e+00 +8.66025e-01 

 Press return to continue. 


 Solving this system yields a unique
 least squares solution, namely   

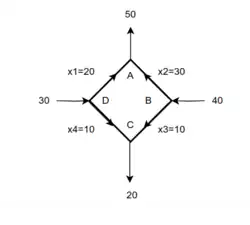
 x = invR * Q_T * b :
+20.00000 
+30.00000 
+10.00000 

 Press return to continue.