Algebra/Chapter 12/Natural Logarithm via Hyperbolic Angle

Natural Logarithm via Hyperbolic Angle

The topics will be developed with analytic geometry in ${\displaystyle Q=\{(x,y):x>0,y>o\}}$, often called the first quadrant of the Cartesian plane. However, a facet of rubber-sheet geometry is invoked with a squeeze parameter, t > 0, that maps Q to itself by (x,y) → (t x, y/t).

Proposition: For all t > 0, and any region of Q, the area of the region after squeezing is the same as the area before.

proof: A rectangle {(0,0), (x,0), (x,y), (0,y)} is mapped to one of the same area (xy). As any region of Q may be approximated by a sequence of sums and differences of such rectangles, the regions’ areas are the same.

Definition: The standard hyperbola ${\displaystyle H=\{(x,y):xy=1\}}$.

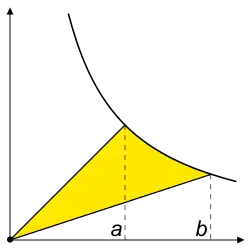
For any P on H, the ray OP is the hypotenuse of a right triangle of area one-half.

Proposition: Given any two points A and B on H, ${\displaystyle A=(a,1/a),\quad B=(b,1/b),}$ the area of the hyperbolic sector to A and B depends only on the ratio b/a.

proof: Apply the squeeze parameter t = 1/a to the sector; the image runs from 1 to b/a. The two sectors have the same area, which depends only on the ratio b/a.

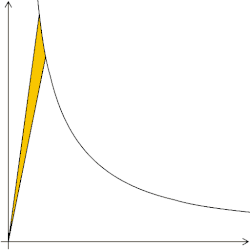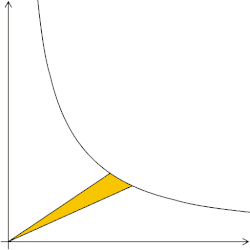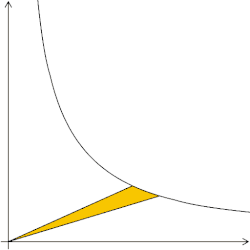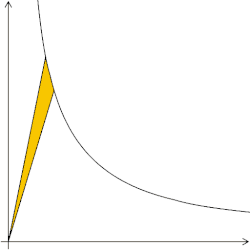
Euler's number: Which hyperbolic sectors have an area of one square unit? Answer: those with b/a = 2.71828…

Definition: A hyperbolic angle size is given by the area of its hyperbolic sector within the standard hyperbola.

Just as circular angle measure is invariant under rotation of its circle, so hyperbolic angle measure is invariant under squeezing.

The shape-shifting nature of squeezing a hyperbolic sector shows that the sectors tend to get very linear when near the asymptotes. The incompatibility of the two angles in the plane shows in the variability of the circular-angle opening as the hyperbolic angle stays constant.

A hyperbolic sector has three sides, but for natural logarithm a four-sided figure is used. The points P and Q on H are projected to S and R, respectively, on the x-axis. The four-sided figure PQRS is styled the area under H. The hyperbolic sector POQ and the four-sided figure PQRS have equal areas: The demonstration involves two right triangles of area one-half, QOR is added, POS taken away, leaving equality of regions.

Definition: For c > 0, the logarithm of c is the area under H from 1 to c, the same as the area of the corresponding hyperbolic sector.

Corollaries: The logarithm of e is one. The area under H over [a,b] is log(b/a).

Proposition: log (ab) = log a + log b

proof: [1, ab] = [1, a] u [a, ab]. The area over [a, ab] is log(ab/a) = log b.

Therefore, the area under H and over [1, ab] is log a + log b.

Definition: a < b means b − a is a positive number.

The ordering of the positive reals with < is conventionally the positive orientation. The opposite orientation (with b − a < 0 ) is then the negative orientation.

Definition: The horns of a hyperbola are the regions between the hyperbola and an asymptote, distant from the origin.

As each horn has infinite area, and a hyperbolic sector may range freely into either with squeezing, a reference point is needed. To set a starting point, the standard convention is to set a = 1. Then with b > 1 (positive orientation), the sector area is taken positively. The other case, 0 < b < 1, has b − a < 0, indicating negative orientation, so the sign of the area of the corresponding sector is taken as negative.

The logarithm function is then negative over the unit interval (0, 1).

A consequence of the symmetry in quadrant Q is the logarithmic identity log (1/p) = − log p .